728x90
1. 데이터베이스 저장과 접근
① 보조기억 장치
| ∘데이터베이스의 저장은 주로 직접 접근 저장 장치(DASD: Direct Access Storage Device)인 자기 디스크를 사용하며 이것은 적은 비용으로 방대한 양의 데이터 저장이 가능함 ∘디스크에 저장하는 가장 기본적인 데이터의 단위는 비트이며, 특정 방법으로 디스크상의 한 영역을 자기화함으로써 0 또는 1의 bit 값을 표현할 수 있음 ∘디스크 팩은 여러 장의 자기 디스크를 묶어서 구성되며, 대형 서버의 경우 수십~수백 GB의 용량을 가지며 그 용량은 계속 증가하는 추세임 ∘디스크는 디스크 표면상의 동심원인 트랙으로 나누어지며 각 트랙은 4~50 KB를 기록할 수 있음. ∘트랙은 블록으로 나누어지며 블록 크기는 한 시스템 내에서 고정되어 있으며 일반적인 블록 크기는 512byte~4096byte 이며, 주기억장치와 디스크간의 데이터 이동 단위가 됨 ∘판독/기록 헤드가 전송할 블록이 있는 트랙으로 이동하고 자기 디스크면이 회전하여 원하는 블록이 판독/기록 헤드 아래에 위치하면 그 블록을 읽거나 씀 ∘디스크 접근 시간 = 탐색시간 + 회전 지연시간( 또는 지연시간 ) + 블록 전송 시간 ∘물리적 디스크 블록 주소는 표면번호, 표면 내 트랙번호, 트랙 내 블록번호로 구성됨 ∘디스크 블록의 읽기나 쓰기에서 탐구시간과 회전 지연 시간이 대부분의 시간을 차지함 ∘연속된 디스크 블록을 전송함에 있어 시간을 줄이기 위해 이중 버퍼링을 사용할 수 있음 ∘이중 버퍼링이란 디스크 블록이 주기억 장치로 전송되면 CPU가 그 블록에 대한 처리가 시작되고, 동시에 디스크 처리기은 다음 블록을 판독하고 다른 버퍼로 전송하는 동시 수행하는 기법으로서, 연속적인 블록들을 주기억 장치에서 디스크로 기록할 때도 사용되어짐 ∘연속적인 디스크 블록상의 데이터를 판독/기록하면, 디스크 접근 시간 중에 탐구시간과 회전 지연시간을 줄일 수가 있고, 처리 중에 대기시간을 줄일 수 있는 장점이 있음 |
※ 자기디스크 내부 구조
 [그림 1] 디스크 상의 여러 섹터 구조 (a) 일정 각으로 분할된 섹터, (b) 동일한 기록 밀도를 유지하는 섹터  [그림 2] 디스크 면과 판독/기록 헤드 (a) 판독/기록 하드웨어를 장착한 단일면 디스크 (b) 판독/기록 하드웨어를 장착한 디스크 |
② 레코드, 블로킹, 파일
| ∎ 레코드(record) ∘데이터는 일반적으로 레코드 형태로 저장되며, 각 레코드는 연관된 데이터 값이나 항목들로 구성되며, 각 값은 하나 이상의 바이트로 구성되며 레코드의 특정 필드에 해당됨 ∘레코드는 엔티티와 엔티티의 애트리뷰트들을 기술함 ∘한 필드의 데이터 타입은 프로그래밍에서 사용되는 표준 데이터 타입들 중의 하나이며 표준 데이터 타입에는 수치, 문자열, 부울(0과 1 또는 TRUE와 FALSE) 데이터 타입이 있고, 때로는 특별하게 코드화 된 날짜, 시간 데이터 타입들도 사용됨 ∘이미지, 비디오, 오디오, 긴 텍스트를 나타내는 방대한 양의 비구조적인 객체들은 BLOB(Binary Large Object)라고 하며, 대개 별도의 디스크 블록들의 풀(pool)에 저장되고 레코드에는 그 포인터만 저장해 둠 ∎ 블로킹(block) ∘디스크와 주기억 장치 사이의 데이터 전송 단위는 하나의 블록이므로 한 파일의 레코드들을 디스크 블록들에 할당하여야 함 ∘블록 크기가 레코드 크기보다 크다면 각 블록에 여러 개의 레코드를 저장하며, 블록크기가 B바이트이라 하고 크기가 R바이트인 고정 길이 레코드들로 구성된 파일에 대하여 B ≥ R인 경우에 블록당 bfr=└B/R┘ 개의 레코드를 저장할 수 있다. 일반적으로 B를 R로 정확히 나눌 수 없으므로 각 블록마다 B - (bfr * R)바이트만큼의 사용되지 않는 공간이 있다. 위에서 bfr은 파일에 대한 블로킹 인수(blocking factor)를 칭함 ∘비사용 공간을 사용하기 위하여 레코드의 일부분을 한 블록에 저장하고 나머지 부분을 다른 블록에 저장할 수도 있음 ∎ 레코드와 파일 ∘파일은 데이터 값이나 항목들로 구성된 레코드의 집합이며, 파일 내의 레코드들이 모두 같을 때 이 파일이 고정 길이 레코드들로 구성되어 있다고 칭함 ∘파일 내의 레코드들의 크기가 서로 다를 때 이 파일은 가변 길이 레코드들로 구성되어 있다고 칭하며, 가변 길이 레코드 파일에서는 가변 길이 필드의 바이트 수를 결정하기 위해 분리 문자를 사용하거나, 필드값 앞에 가변 길이 필드의 바이트 길이를 기록함 ∘레코드를 하나 이상의 블록에 걸쳐서 저장하는 방식을 신장(spanned)조직이라 하며, 특히 레코드 하나의 크기가 한 블록의 크기보다 클 경우 신장(spanned)조직을 사용하여야 한다. 이에 반하여 레코드가 블록 경계를 넘지 않도록 저장하는 방식을 비신장(unspanned) 조직이라 칭함 ∘가변길이 레코드의 경우에는 신장 또는 비신장 조직을 사용할 수 있음 ∘평균 레코드 크기가 클 경우에는 각 블록내의 손실 공간을 줄이기 위하여 신장조직을 사용하는 것이 유리함 |
※ 블록과 레코드
 [그림 3] 레코드 조직의 유형 (a) 비신장 조직 (b) 신장 조직 |
③ 데이터베이스 접근 - 파일관리자, 디스크관리자
| ∎ 데이터베이스의 디스크 접근 과정 ∘DBMS는 사용자가 요구하는 레코드를 결정함 ∘파일관리자에게 저장레코드의 검색을 요청함 ∘파일관리자는 저장레코드가 들어있는 페이지를 결정함 ∘디스크 관리자에게 그 페이지의 검색을 요청함 ∘디스크 관리자는 그 페이지의 물리적 위치를 결정함 ∘디스크에 입출력 명령을 내림 |

| ∎ 디스크관리자의 역할 ∘기본 입출력 서비스 (basic I/O service) 모듈 : 모든 물리적 I/O 연산에 대한 책임을 지며 최종적으로 물리적 디스크 주소로서 처리되며, 디스크 관리자는 운영체제의 구성요소임 ∘파일 관리자를 지원하며, 파일 관리자를 장비에서 독립시키는 역할을 한다. 즉 물리적 디스크 주소와 페이지 번호 간에 사상(mapping)을 시켜서 그 연산을 수행함 ∘페이지라 함은 디스크와 주기억 장치 간에 입출력단위가 되는 블록을 말하며, 보통 2KB, 4KB 혹은 8KB 등의 단위로 할당되며, 각 페이지는 디스크 내에서 유일한 페이지 번호로 식별됨 ∘페이지 관리 연산, 즉 파일 관리자가 디스크 관리자에게 명령할 수 있는 연산 ① 페이지 세트 S 로부터 페이지 P의 검색 ② 페이지 세트 S 내에서 페이지 P의 교체 ③ 페이지 세트 S 에 새로운 페이지 P의 첨가(자유공간 페이지 세트의 빈 페이지를 할당) ④ 페이지 세트 S 에서 페이지 P를 제거 (자유공간 페이지 세트로 반환) ∘위의 ③, ④번은 디스크 관리자의 필요에 따른 연산이며, ①, ② 번은 파일 관리자의 요청에 의한 연산으로 구분됨 ∘디스크에는 통상 실린더 0, 트랙 0에는 디스크 디렉터리(disk directory) 또는 페이지 세트 디렉터리(page set directory)가 있으며, 이곳에는 디스크에 있는 모든 페이지 세트의 리스트와 각 페이지 세트의 첫 번째 페이지에 대한 포인터 저장되어 있음 ∎ 파일 관리자의 역할 ∘파일 관리자는 DBMS가 디스크를 저장 파일들의 집합으로 취급할 수 있도록 지원함 ∘저장 파일(stored file)이란 한 타입의 저장레코드 어커런스들의 집합으로 한 페이지 세트는 보통 하나 이상의 저장 파일을 포함하고 그것은 파일 이름 또는 파일 ID로 식별됨 ∘저장 레코드란 레코드번호 또는 레코드 ID(RID: Record Identifier)로 식별되고 전체 디스크 내에서 유일함 ∘RID는 페이지 번호와 오프셋(슬롯번호)로 구성됨 ∘파일 관리자는 OS의 한 구성요소 또는 DBMS와 함께 패키지화 되어서 운영되기도 함 ∘파일 관리자의 파일 관리 연산, 즉 DBMS가 파일관리자에 명령할 수 있는 연산 ① 저장 파일 f에서 저장 레코드 r을 검색함 ② 저장 파일 f에 있는 저장 레코드 r을 대체함 ③ 저장 파일 f에 새로운 레코드를 첨가하고 새로운 레코드 RID, r을 반환함 ④ 저장 파일 f에서 저장 레코드 r을 제거함 ⑤ 새로운 저장 파일 f를 생성함 ⑥ 저장 파일 f를 제거함 |
※ 레코드 ID(RID)
 [그림 5] RID의 구조 ∘RID = (페이지 번호 p, 오프셋(슬롯번호)) ∘오프셋은 페이지 내에서의 레코드 위치(byte)를 표현함 ∘레코드가 한 페이지 내에서 이동할 때마다 오프셋의 내용(포인터)만 변경 ∘최악의 경우 두 번째 접근으로 원하는 레코드 검색가능 즉, 해당 페이지가 오버플로가 되어 다른 페이지로 저장된 경우 두 번 접근될 수 있음 |
④ RAID 및 SANs 기술
| ∎ RAID 기술을 이용한 병렬 디스크 접근 ∘여러 개의 작고 독립적인 디스크를 배열로 구성하여 하나의 고성능 디스크처럼 동작하도록 하는 것으로서 디스크의 성능 향상을 위해 병렬성을 사용하는데, 이 개념을 데이터 스트라이핑이라 함 ∘데이터 스트라이핑은 여러 개의 디스크가 하나의 크고 빠른 디스크처럼 보이도록 데이터를 다중 디스크로 투명하게 분산시키는 역할을 함 ∘신뢰성을 향상시키는 첫 번째 방법은 데이터를 두 개의 동일한 물리적 디스크에 중복해서 기록하는 반사(또는 그림자) 기법을 사용하는 것이고, 두 번째 방법은 디스크 오류 발생시 손실된 정보를 재구축하는 데 사용할 부가 정보를 저장하는 것임 ∘두 번째 방법의 부가 정보를 계산하기 위해서 패리티 비트나 해밍 코드 같은 특별한 코드를 포함한 에러 검출 코드를 사용하며, 중복된 정보를 디스크 배열상에 분산시키기 위해 몇 개의 디스크에 여분의 정보를 저장하는 방식과, 모든 디스크에 균등하게 여분의 정보를 저장하는 방식이 있으며, 후자의 방식이 더 좋은 부하 균등을 제공함 ∎ 저장 영역 네트워크(SANs) ∘고성능인 저장 장치에 대한 요구가 점점 늘어나고, 정적이고 고정된 데이터 센터 중심에서부터 더 유연하고 동적인 구조로의 전환이 필요성 때문에 대규모 조직체들은 저장 영역 네트워크(Storage Area Networks : SANs) 개념으로 점차 옮겨가고 있음 ∘SANs에서는 온라인 저장 주변장치들이 초고속 네트워크에 노드들로 구성되어 있고, 매우 유연한 방법으로 서버들에 연결되거나 분리될 수 있으며, 이것은 저장 시스템들이 서버로부터 더 먼 거리에 위치할 수 있도록 해 주고, 서로 다른 성능과 연결 옵션들을 제공함 ∘SANs의 장점은 광섬유 채널 허브들과 스위치들을 사용하여 서버들과 저장 장치들간의 유연한 다대다 연결과 적절한 광섬유 케이블을 사용하여 서버와 저장 시스템 사이에 10km까지 거리가 떨어지는 것이 가능하며 새로운 주변장치와 서버들을 유연한 방법으로 연결하거나 분리하는 기능을 가지고 있음 |
2. 파일 조직 방법
① 비순서 파일과 순서 파일
| ∎ 비순서 파일 ∘heap file이나 pile file로 불리기도 하며, 새로운 레코드는 파일의 마지막에 삽입하므로 삽입이 매우 효율적임 ∘레코드를 탐색하기 위해서는 선형 탐색 기법을 사용해야 하며, 이 기법은 평균파일 블록의 반을 탐색하기 때문에 아주 비효율적이고 그리고 어떤 필드 값의 순서대로 레코드를 판독하기 위해서는 해당 파일의 레코드들을 정렬시켜야 함 ∘비신장 블록과 연속할당 방식을 사용하는 비순서 고정길이 레코드들로 구성된 파일에서는 레코드의 위치(순번)을 이용하여 레코드를 접근할 수 있으며, 이런 방식으로 접근할 수 있는 파일을 상대 파일이라고 함 ∎순서 파일 ∘순차파일(sequential file)이라고도 하며, 파일에 레코드들을 순서 필드의 값에 따라 정렬됨 ∘레코드들이 정렬된 형태로 추가되어야 하기 때문에 삽입 비용이 비싸며, 효율적으로 작업하기 위해 오버플로 파일 또는 트랜잭션 파일을 사용하는 것이 좋지만, 이 방식은 정기적으로 주 파일에 합병시켜야 됨 ∘이진 탐색은 레코드의 순서 필드값에 따른 탐색의 경우 사용되며, 평균적으로 Log2b개의 블록을 접근하는 이진 탐색은 선형 탐색보다 더 좋은 성능을 보임(b는 블록의 총 개수) ∘정렬된 키 값의 순서대로 판독하는 연산이 매우 효율적이며, 반면에 레코드 삽입과 삭제는 레코드를 물리적으로 정돈된 상태를 유지해야 하므로 비용이 매우 큼 ∘순서 파일 방식에서 비순서 필드 값을 기반으로 레코드들을 임의 접근하거나 순서 접근하기 어려우며,. 이 경우에 임의 접근은 선형 탐색을 사용하고, 순서 접근은 파일을 정렬한 복사본을 사용해야 함 ∘삽입을 효율적으로 수행하기 위해 오버플로 파일 또는 트랜잭션 파일이라는 임시 비순서 파일에 기록한 후 주파일 또는 마스터 파일과 정기적으로 합병 함 ∘레코드 삭제시 빈 공간을 메우기 위해 레코드들을 이동하거나 삭제 표시자를 사용함. ∘순서 필드 값을 수정하는 연산은 그 레코드를 삭제하고 새로운 순서 필드 값을 갖는 레코드를 삽입함 ∘기본 인덱스라고 부르는 부가적인 접근 경로를 파일과 함께 사용하는 경우가 아니면 데이터베이스 응용에서 순서 파일을 거의 사용하지 않음 |
※ 기본파일 구조에 대한 평균 접근 시간
| 유형 | 접근방법 | 특정레코드 접근 평균시간 |
| Heap(Unordered) | Sequential scan (Linear Search) |
b/2 |
| Ordered | Sequential scan | b/2 |
| Binary Search | log2b |
[표 1] 기본파일 구조에 대한 평균 접근 시간 비교표
② 해싱 파일
| ∎해싱 파일 구조 ∘해싱 기반으로 조직된 파일을 해시 파일(hash file) 또는 직접 파일(direct file)이라고 함 ∘해시 함수 또는 난수화 함수라고 하는 함수 h를 레코드의 해시 필드값에 적용하여 레코드를 저장하고 있는 디스크 블록의 주소를 산출함 ∘대부분의 레코드에 대해 한 번의 블록 접근으로 원하는 레코드를 검색하는 매우 효율적인 방식이며, 파일의 키 필드로 해시 필드를 사용할 경우 이를 해시키라고 함 ∘프로그램에서 어떤 필드값을 사용하여 레코드들의 그룹을 배타적으로 접근하고자 할 때 내부 탐색 구조로 해싱을 사용함. ∘내부 파일에서 해싱은 일반적으로 레코드들의 배열을 이용하여 해시 테이블로 구현함 ∘해시 필드 공간이 주소 공간보다 매우 크기 때문에 대부분의 해시 함수는 서로 다른 해시 필드값을 항상 서로 다른 주소로 사상하지는 못하는 문제점이 있음 ∘삽입하려는 새로운 레코드의 해시 필드 값이 다른 레코드가 이미 점유하고 있는 주소로 해싱될 때 충돌이 발생하며 이 경우 새로운 레코드를 삽입할 다른 위치를 찾아야 하는데 이를 충돌 해결이라 함 ∘해시 테이블을 70%에서 90% 정도 사용하도록 유지할 때 충돌 횟수도 줄이고, 공간 낭비도 줄일 수 있음 ∎충돌 해결 기법 ∘개방 주소 지정(Open addressing): 해시 주소가 가리키고 있는 위치부터 시작하여 빈위치를 찾을 때까지 순차적으로 그 이후의 위치들을 조사함 ∘체인(Chaining): 오버플로 영역에 새로운 레코드를 저장하고 다른 레코드가 이미 점유하고 있는 해시 주소 영역의 포인터에 오버플로 영역의 주소를 지정하여 충돌을 해결함 ∘다중 해싱(Multiple hashing): 충돌이 발생하지 않을 때까지 여러 개의 해시 함수를 적용한다. 충돌시 필요하면 개방 주소 지정 방법을 사용함 |
 [그림 6] 버켓번호 들을 디스크 블록 주소들과 사상 ∘목표 주소 공간을 같은 크기의 버켓들로 구성하고, 각 버켓에는 다수의 레코드들을 유지함. ∘버켓은 디스크 블록 한 개나 연속적인 블록인 클러스터 한 개의 크기를 갖임 ∘해시 키가 K 인 레코드는 해시 함수 i = h(K)에 의해 결정된 버켓 i 에 저장 ∘가득 찬 버켓으로 새로운 레코드가 해시 될 경우 충돌이 발생되며 충돌된 레코드는 오버플로 버켓에 저장, 각 버켓에서 오버플로된 레코드들은 연결 리스트로 구성 함 ∘버켓의 수가 고정되어 있기 때문에 파일의 레코드수가 버켓 공간에 비해 너무 적으면 공간 낭비가 초래되고, 너무 많으면 빈번한 충돌 발생의 문제가 발생함 ∘해시 키에 따른 순차적 접근은 매우 비효율적이며 레코드의 정렬이 요구됨 ∘정적 해싱은 해시 주소 공간이 고정되어 파일을 동적으로 확장하고 축소하는 것이 어렵기에 이 문제를 해결하기 위한 기법으로는 확장가능 해싱, 선형 해싱 등이 있음 ∘동적 및 확장 해싱 파일의 개념은 이진수로 된 비트열을 구성하고 레코드 해시값에서 선행하는 비트들의 값을 기반으로 레코드들을 버켓들에 분배하고 확장 가능하도록 하는 것임 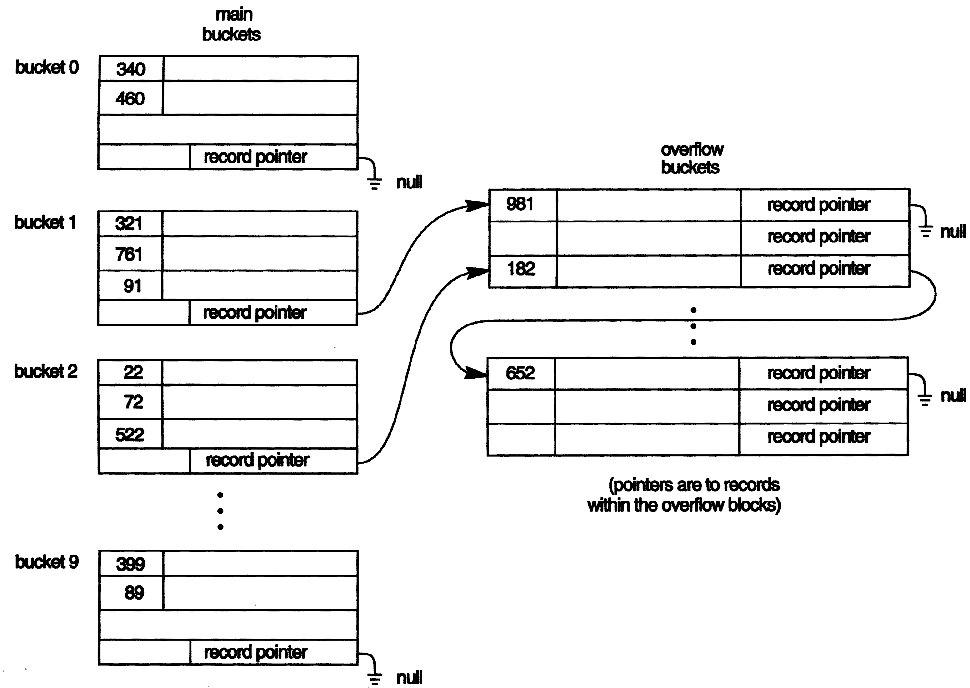 [그림 7] 체인 방법을 사용한 버켓 오버플로 처리 |
③ 인덱스 파일
| ∘인덱스를 통해 데이터 레코드를 접근하는 인덱스 파일(indexed file)은 인덱스 파일(index file)과 데이터 파일(data file)로 구성됨 ∘인덱스 파일은 하나의 인덱스를 사용하고 순차 파일과 직접 파일을 결합한 형태 임 ∘순차 데이터 파일(sequential data file)은 레코드가 순차적으로 정렬되었으며 이것은 레코드 집합 전체에 대한 순차 접근 요구를 지원하는데 사용하며, 인덱스(index)는 레코드들에 대한 포인터로서 개별 레코드들에 대한 임의 접근 요구를 지원하는데 사용함  [그림 8] 인덱스 파일의 구조 ∘다중 키 파일(multikey file)은 데이터를 중복시키지 않으면서 여러 방법으로 데이터를 접근할 수 있는 다중 접근 경로를 제공하며 이것에는 각 응용에 적절한 인덱스를 만들어 구현하는 역 파일(inverted file)과 하나의 인덱스 값마다 하나의 데이터 레코드 리스트를 구축하는 다중 리스트 파일(multilist file)이 있음  [그림 9] 다중 키 파일(multikey file) |
3. 파일의 인덱스 구조
① 인덱스의 구조 및 그 유형
| ∎인덱스의 구조 ∘인덱스는 보통 파일내의 한 필드에 대해 정의되지만, 경우에 따라서는 여러 필드에 대해 정의될 수도 있음 ∘인덱스는 <필드 값(레코드 키 값), 레코드에 대한 주소(포인터)>로 구성된 엔트리들을 저장한 파일을 칭하며, 파일에 대한 접근 경로(access path) 라고 불림 ∎인덱스의 유형 ∘기본 인덱스(primary index) : 순서파일에 대해 정의할 수 있는 인덱스이며, 보통 이 데이터 파일은 키 필드 순으로 정렬돼 있어야 하며, 데이터 파일의 각 블록에 대해 하나의 엔트리를 가지며, 블록 앵커라 불리는 각 블록의 첫 번째 레코드에 대한 키 필드 값을 엔트리로 갖는다. 각 블록의 마지막 레코드를 블록 앵커로 사용하는 방식을 이용할 수도 있다.전체 탐색 값이 아니라 데이터 파일의 각 블록에 대해 하나의 엔트리 (즉, 블록의 앵커 레코드에 대한 키 값)을 가지므로, 기본 인덱스는 비밀집(희소) 인덱스로 분류됨 ∘보조 인덱스(secondary index) : 기본 접근 방법이 이미 존재하는 파일을 접근하는 보조 수단을 제공하며, 후보 키나 모든 레코드에 대해 유일한 값을 갖는 필드 또는 중복된 값을 갖는 키가 아닌 필드에 대해 만들 수 있음 ∘집중 인덱스(clustered index) : 데이터 레코드의 물리적 순서가 인덱스 엔트리 순서와 동일하게 유지하도록 구성된 인덱스를 말하며, 같은 인덱스 키 값을 가진 레코드는 물리적으로 인접하게 되어서 검색이 아주 효율적임 ∘비 집중 인덱스(unclustered index) : 집중 형태가 아닌 인덱스로서 하나의 데이터 파일에 여러 개 생성이 가능함 ∘밀집 인덱스(dense index) : 데이터 레코드 하나에 대해 하나의 인덱스 엔트리가 만들어지는 인덱스로서 역 인덱스(inverted index)는 보통 밀집 인덱스 형태로 만듬 ∘희소 인덱스(sparse index) : 데이터 파일의 레코드 그룹 또는 데이터 블록에 하나의 엔트리가 만들어지는 인덱스를 칭함 |
※ 집중 인덱스 (일종의 희소 인덱스)
 [그림 10] 키가 아닌 필드가 물리적으로 정렬된 클러스터링 인덱스의 예 |
② B 트리
| ∎차수 m인 B 트리의 특성 ∘ 공백이거나 높이가 1이상인 m-원 탐색 트리(m-way search tree) ∘ 루트와 리프(leaf)를 제외한 내부 노드는 최소 ⌈m/2⌉, 최대 m개의 서브트리를 가짐 (적어도 ⌈m/2⌉-1개의 키 값을 가짐) ∘ 루트는 그 자체가 리프가 아닌 이상 적어도 두 개의 서브트리를 가짐 ∘ 모든 리프는 같은 레벨에 있음, 즉 균형 트리 임 ∎B 트리의 노드의 구조 및 특성 ∘B 트리 노드의 구조 <n, P0, <K1, A1>, P1, <K2, A2>, P2, … , Pn-1, <Kn, An>, Pn> ∘n : 키 값의 수 ( 1≤n<m ) ∘P0, …, Pn : 서브트리에 대한 포인터 ∘K1, …, Kn : 키 값 ∘각 키 값(Ki)은 그 키 값을 가지고 있는 레코드에 대한 포인터 Ai를 함께 포함 ∘한 노드 안에 있는 키 값들은 오름차순 ∘Pi (0≤i≤n-1)가 지시하는 서브트리에 있는 모든 노드들의 모든 키 값들은 키 값 Ki+1보다 작음 ∘Pn이 지시하는 서브트리에 있는 노드들의 모든 키 값들은 Kn보다 큼 ∘Pi (0≤i≤n)가 지시하는 서브트리들은 모두 m-원 서브 탐색 트리 ∎ B 트리에서의 연산의 종류 ∘ 직접 탐색 : 키 값에 의한 분기 ∘ 순차 탐색 : 중위 순회 ∘ 삽입, 삭제 : 트리의 균형을 유지해야함 ∘ 분할 : 노드 오버플로 발생시 ∘ 합병 : 노드 언더플로 발생시 |
※ B 트리 구조 예
 [그림 11] 3차 B 트리의 구조 |
③ B+ 트리
| ∎B+ 트리의 구조 ∘B+ 트리는 인덱스 세트과 순차 세트로 구조로 되었으며, 인덱스 세트(index set)는 트리 구조에서 내부 노드 부분이며, 리프에 있는 키들에 대한 경로 제공하는 역할을 하고, 순차 세트 (sequence set)는 트리 구조에서 리프 노드에 해당되며 모든 키 값들을 포함하고 순차 세트는 순차적으로 연결되어서 순차 처리를 지원해 줌 ∎B+ 트리의 노드의 구조 및 특성 ∘B+ 트리 노드의 구조
<n, P0, K1, P1, K2, P2, … , Pn-1, Kn, Pn> ∘n : 키 값의 수 ( 1≤n<m ), 여기서 m은 트리의 차수를 의미함 ∘P0, …, Pn : 서브트리에 대한 포인터 ∘K1, …, Kn : 키 값 ∘루트는 0 또는 2에서 m개 사이의 서브트리를 가짐 ∘루트와 리프를 제외한 모든 내부 노드는 최소 ⌈m/2⌉개, 최대 m개의 서브트리를 가짐 ∘리프가 아닌 노드에 있는 키 값의 수는 그 노드의 서브트리 수보다 하나 적음 ∘모든 리프 노드는 같은 레벨 ∘한 노드 안에 있는 키 값들은 오름차순 ∘Pi, (0≤i≤n-1)가 지시하는 서브트리에 있는 노드들의 모든 키 값들은 키 값 Ki+1보다 작거나 같다. ∘Pn이 지시하는 서브트리에 있는 노드들의 어떤 키 값도 키 값 Kn보다 크다. ∘리프 노드는 모두 링크로 연결되어 있다. ∘리프 노드의 구조 <q, <K1, A1>, <K2, A2>, … , <Kq, Aq>, Pnext> ∘Ai : 키 값 Ki를 가지고 있는 레코드에 대한 포인터 ∘q : ⌈m/2⌉≤ q ∘Pnext : 다음 리프 노드에 대한 링크 |
※ B+ 트리 구조 예
 [그림 12] 3차 B+ 트리의 구조 |
| ∎B 트리와의 차이점 ∘인덱스 세트에 있는 키 값은 리프 노드에 있는 키 값을 찾아가는 경로만 제공하기 위해서 사용함 ∘인덱스 세트에 있는 키 값은 사실상 모두 순차 세트에 다시 나타남 ∘인덱스 세트의 노드와 순차 세트의 노드는 그 내부 구조가 서로 다름 ∘리프 노드는 키 값과 이 키 값을 포인터가 함께 저장됨 ∘인덱스 세트에 있는 노드는 키 값만 저장됨 ∘노드에 저장할 수 있는 원소의 수도 서로 다름 ∘순차 세트의 모든 노드가 순차적으로 서로 연결된 연결 리스트로 구성됨 ∘B+ 트리는 B 트리에 비해서 순차 접근이 효율적임 |
4. 다차원 공간 파일
① 격자 파일의 개요
| ∘레코드의 삽입과 삭제가 자주 발생되지 않는 정적상황과 삽입과 삭제가 빈번히 발생하는 동적상황에 잘 적용되는 파일 구조 ∘격자 파일에 적용되는 질의 검색연산 - 완전 일치 질의 : 레코드의 모든 검색 키에 대한 값이 명세 된 경우 - 범위 질의 : 특정 검색 키 값으로 범위 수식이 명세 된 경우 - 부분일치 질의 : 몇 개의 검색 키에 대한 값이 조건으로 명세 된 경우 ∘X-Y 평면상의 점 파일은 아래 표2와 같음 ∘격자 파일의 구성 - X-Y 평면에 존재하는 점들을 나타냄 - 좌표 값을 나타내는 애트리뷰트 X, Y와 점을 식별할 수 있는 PID를 가짐 - X 좌표 : 0 - 20, Y 좌표 : 0 - 10 사이의 값으로 구성 - PID는 하나의 영문자와 하나의 숫자로 구성 ∘인덱스 엔트리 = (키 값의 범위, 페이지 번호)로 구성 |
[표 2] X-Y 평면상의 점 파일
| PID | X | Y |
| E1 | 2 | 4 |
| M1 | 4 | 6 |
| Z1 | 16 | 2 |
| E2 | 7 | 2 |
| W1 | 18 | 8 |
| K1 | 9 | 4 |
| H1 | 8 | 8 |
| A1 | 13 | 9 |
| Z2 | 6 | 4 |
| L1 | 4 | 2 |
| E3 | 15 | 8 |
② 격자 파일의 인덱스
| ∘[표 2]의 레코드를 위에서부터 차례로 삽입시키는 인덱스 파일에 관한 설명을 함 - 전제조건; 데이터 페이지에는 최대 3개 레코드만 저장할 수 있음 - PID가 가질 수 있는 범위가 값의 최대범위인 (A0<PID≤Z9)까지 설정했을 경우 페이지 번호 P1에는 E1데이터가 삽입이 됨 - E1, M1, Z1 3개를 계속 P1에 삽입할 수 있으나, E2를 입력하려면, 오버플로가 발생하기 때문에 P2를 할당 받게 됨. 즉, P1은 P1과 P2로 키 분할이 되며, 분할점은 L9가 됨  [그림 13] 인덱스 파일 상태 - 도중에 삭제가 발생하여 체이지 적재율이 낮을 경우에는 합병이 발생됨 ∘키값의 범위를 선형 눈금자(linear scale), 페이지 번호를 격자 배열(grid array)라고 함 ∘선형 눈금자와 격자 배열을 격자 디렉토리(grid directory)라 하고, 가장 작은 공간을 격자 블록이라고 함 ∘아래 그림은 격자 분할 과정의 일부를 나타낸 그림으로서, W1은 P2에 삽입할 수 있고, 이전 단계에서 K1은 P1에 오버플로가 발생되어서 Y축을 중심으로 Y=5로 이분하게 되었으며, 새로운 P3을 할당받아서 빗금 친 부분의 레코드를 P3으로 이동시킨 상태임 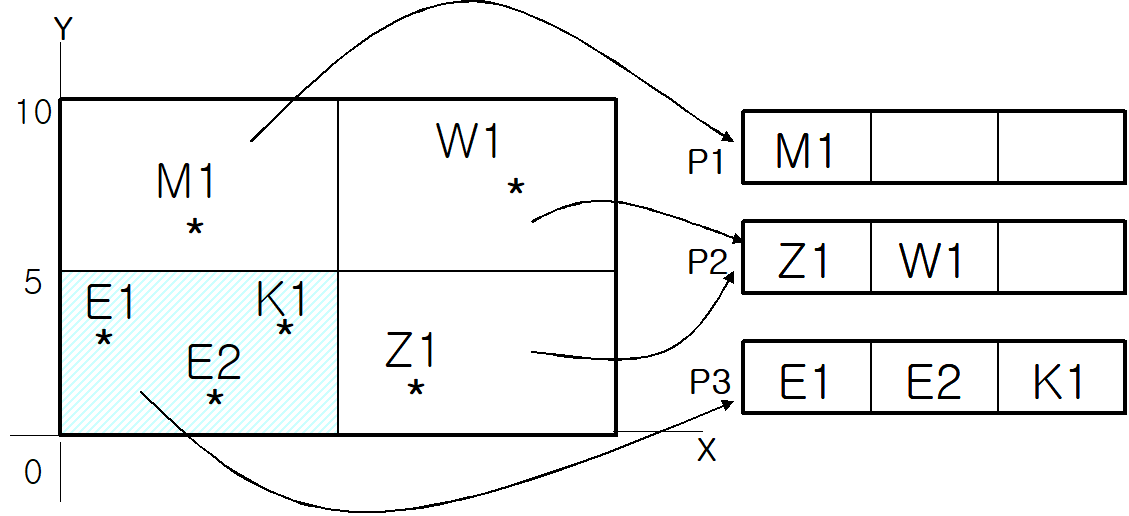 [그림 14] 격자 분할의 예 ∘격자 파일은 인덱스의 키의 개수가 작을 때 효율적(10개 미만) ∘각 키들이 가질 수 있는 값의 범위가 크고 균등하게 분포되어 있을 때 효율적 |
③ K-D 트리
| ∘K-차원(K-Dimensional)트리를 의미하며, 기본 키에 의한 검색과 보조키에 의한 검색을 하나의 구조로 결합 ∘보조키 값의 범위에 따라 레코드를 검색할 때 적용 가능 ∘하나의 애트리뷰트에 대하여 비교하는 이진 트리와 달리 두개의 애트리뷰트를 두 레벨마다 번갈아 가며 비교함 ∘탐색 시 범위 탐색을 함으로써 하나 이상의 탐색 경로의 선택이 가능 ∘레코드의 비교 결과는 ≤또는 > 중 하나를 선택하여 “ ≤ ” 일 경우 왼쪽, “ 〉”일 경우 오른쪽 가지를 따라 비교 검색 ∘2-D트리에서는 두 개의 차원(애트리뷰트)을 이진 트리의 두 레벨마다 번갈아 가며 비교하고, 3-D트리인 경우는 3개의 서로 다른 차원을 세 레벨마다 차례로 번갈아 가며 비교하고, 4-D 트리는 4개의 레벨을 이와 같은 방법으로 수행함 ∘김씨 중간성적이 이씨의 중간성적보다 작으므로 (34<36) 왼쪽 가지의 자식노드로 삽입 ∘차씨 중간성적은 김씨의 중간성적보다 크므로(38>34) 오른쪽 가지의 자식노드로 삽입 ∘두 번째 2진트리가 가득 찬 상태이기에 박씨 삽입은 중간성적 37을 비교 오른쪽 가지를 타고 내려가서 다시 차씨와 기말성적을 비교하여 차씨(51)<박씨(54) 이므로 오른쪽 자식노드 ∘2-D 트리의 각 노드는 실제로 2차원 탐색공간을 두 부분으로 나누기에 트리 하단부 탐색공각은 계속적으로 좁아짐 ∘2-D 트리의 장점 - 2-D 트리는 검색을 위한 탐색공간을 줄이는 일종의 필터링 기법 - 2-D 트리는 탐색해야 할 필요가 있는 데이터의 양을 감소시킴으로써 탐색성능을 향상 시키자는 것임 ∘2-D 트리의 단점 - 모든 검색필드가 균등하게 분포되어 있지 않은 경우에는 성능의 효율성 감소 - 오버플로우 페이지들이 파일 내에 많이 생성되면 대표 레코드를 변경하고 인덱스를 재구성해서 데이터들을 다시 적재해야 함 |
[표 3] 데이터 레코드 2-D의 예
| 이름 | 중간성적 | 기말성적 | ... |
| 이씨 | 36 | 48 | |
| 김씨 | 34 | 52 | |
| 차씨 | 38 | 51 | |
| 박씨 | 37 | 54 | |
| .. | ... | .. | ... |
④ K-D-B 트리, 사분트리
| ∎K-D-B 트리 ∘K-D-B 트리의 특징 - 범위질의(range query)를 통해 다중 키 레코드를 효율적으로 검색하기 위한 기법 - B 트리와 K-D 트리의 특징을 결합 - B 트리와 같이 루트 노드에서 단말 노드까지의 경로 길이가 모두 같은 완전 균형 트리 - 각 노드는 페이지에 저장되며 이는 페이징 기법으로 보조 기억장치를 효율적으로 사용 ∎사분트리 ∘공간을 순환적으로 분해하는 특성을 갖는 계층적 자료구조로 다음 기준으로 구분됨 - 표현하고자 하는 자료의 유형 . 점, 영역, 곡선(curve), 개체의 표면(surface), 개체의 볼륨(volume)데이터 등 . 곡선이나 표면과 같이 개체의 경계를 표현하는 경우와 영역이나 볼륨과 같이 개체의 내부를 표현하는 경우에 따라서 자료구조가 다름 - 공간 분해 과정의 원칙 . 각 레벨마다 공간을 일정한 크기의 동일한 부분들로 분해 하거나, 또는 입력 자료 값에 따라 서로 다른 크기의 공간으로 분해하는 두 가지 경우 . 컴퓨터 그래픽스 분야 : 영상 공간 계층과 객체 공간 계층 방법이 있음 - 해상도(resolution): 분해 과정의 반복 적용 여부 ∘개념 - 사분트리는 2차원의 영역 데이터를 표현하기위해 사용 - 이러한 응용에 사용되는 사분 트리를 영역 사분트리라 칭 함 - 이미지를 표현하는 2진수의 배열을 연속적으로 동일한 크기의 사분면으로 분할 - 배열이 완전히 1 또는 0으로만 구성되지 않으면 블록이 모두 동일하게 1 또는 0으로 구성될 때 까지 다시 사분면, 부속 사분면들로 분할 - 영역 사분트리는 가변 해상도를 갖는 자료구조로 특정 지움  [그림 15] 영역 사분트리를 이용한 이미지 표현의 예 ∘점 사분 트리 - 다차원 데이터를 처리할 수 있도록 이진 탐색 트리를 일반화 - 점 데이터를 표현하기 위해 사분 트리의 한 변형인 점 사분 트리 사용 - K-D 트리나 격자 파일처럼 2차원 점 데이터에 대한 인덱스로 활용 |
⑤ R 트리(1)
| ∘ R 트리 필요성 - 비 정형화된 데이터베이스의 응용 중에서 CAD와 지리 데이터 응용 등에서 필요한 공간 데이터를 다 루기 위해서는 데이터의 공간적 위치에 따라 신속하게 데이터 항목을 검색하도록 하는 인덱스 기법이 필요 - 기존 인덱스 기법들은 다차원 공간에 위치하며 크기가 있는 데이터 객체들을 다루기에 부적합 - 공간 데이터 객체들은 다차원 공간에 위치하며 점 위치만으로는 제대로 표현할 수 없음 ∘ R 트리 인덱스 구조 - B 트리와 유사하게 인덱스 레코드들로 구성되는 높이 균형 트리 - 리프 노드는 데이터 객체에 대한 포인터를 포함 - 공간 탐색 시 적은 수의 노드만을 방문하여 원하는 객체를 탐색할 수 있도록 설계 - 리프 노드는 <I, 주소> 형태로 인덱스 레코드 엔트리를 포함 - 주소는 데이터 레코드에 대한 포인터를 의미 - I는 K 차원의 사각형으로 인덱스 되는 공간객체의 경계 사각형(MBR) - 리프가 아닌 중간 노드들은 <I, 자식 포인터>와 같은 엔트리들을 포함 - 자식 포인터는 R 트리에서 하위 레벨 노드의 주소, I는 하위 레벨 노드의 엔트리에 있는 모든 사각형을 포함하는 사각형 ∘R 트리는 MBR(Minimum Bounding Region)을 계층 형태로 표현하며, 그 종류는, - 저차원: R Tree, R+ Tree, R* Tree, Hilbert R Tree 등 - 고차원: TV Tree, X Tree, SS Tree, SR Tree, CIR Tree 등  [그림 16] R 트리의 예 ∘R 트리가 표현한 사각형들 사이의 포함(coverage)과 겹침(overlap)의 관계 - 포함 관계 : 해당 레벨의 노드들에 관련된 모든 사각형의 전체 영역으로 정의 - 겹침 관계 : 두개 이상의 노드들에 공통으로 속하는 전체 영역으로 정의 |
⑥ R 트리(2)
| ∘R 트리의 분석 - K-차원에서 데이터를 처리하기 위한 B 트리의 확장으로서 중간 노드와 리프 노드들로 구성된 높이 균형 트리 - R 트리에 대한 탐색을 고려할 때는 포함관계와 겹침 관계의 개념이 매우 중요함 - 탐색은 포함과 겹침 관계가 모두 최소일 때 가장 효율적임 - 겹침 관계를 최소로 유지해야 하나 동적으로 분할하는 동안에 겹침 관계의 최소화 유지의 어려움 ∘R* 트리 - R 트리의 변형, 삽입이나 삭제 연산 시 부모 노드의 사각형이 효율적으로 확장될 수 있도록 하는 트리 - R* 트리는 면적의 최소화 기준뿐만 아니라 몇 가지의 고려사항을 더 적용하는 트리 . 사각형의 면적을 최소화 . 사각형들 간의 겹침을 최소화 . 사각형의 둘레 길이의 합을 최소화 . 기억장소의 이용률을 최적화 ∘R+ 트리 - R 트리에 대한 탐색에서는 최소 포함과 최소 겹침이 성능향상에 매우 중요한 역할 - R+ 트리는 겹침 관계를 줄이기 위한 R 트리의 변형으로서 R 트리에서의 겹침 관계를 제거한 인덱스 구조 - 특징 . 루트노드는 최소 두개의 엔트리를 가짐 . 같은 레벨의 노드 간에 겹침이 없음 . 비단말 노드의 MBR은 하위 노드들의 MBR을 모두 포함 . 인덱스 된 사각형의 집합은 오버랩 되는 모든 단말 노드들에 할당 . 객체들은 겹치거나 포함되는 모든 단말 노드에 할당되며 이로 인해 공간 분할 색인구조에서처럼 한 객체는 여러 단말 노드에 포함될 수 있음 . 겹침이 없으므로 점 질의 시 트리의 레벨만큼의 노드만 접근하면 됨 . 하나의 객체가 여러 노드에 중복 저장될 수 있음 . 부모 노드의 분할로 인해 자식 노드도 분할해야 하는 하향연쇄 분할(downward cascading split)이 발생함 ∘R+ Tree와 R Tree 비교 - R+ Tree는 겹침을 없애는 대신 트리의 높이를 증가, 공간 사용율의 증가 - R Tree는 R+ Tree에 비해 경로의 길이가 짧음, 트리의 탐색 시 여러 경로를 탐색 |
■ 요약정리
| ∘디스크 상에 데이터는 블록단위로 저장되며, 하나의 디스크 블록을 접근하는 데는 많은 시간이 소요됨 ∘디스크 접근 시간 = 탐색시간 + 회전 지연시간( 또는 지연시간 ) + 블록 전송 시간 ∘한 파일을 구성하는 레코드들은 고정길이 또는 가변길이, 신장 또는 비신장, 동일 또는 혼합 타입으로 레코드를 분류할 수 있음 ∘데이터베이스의 디스크 접근 과정에는 시스템 소프트웨어인 파일관리자와 디스크관리자가 그 처리를 담당해 줌 ∘ RAID란 여러 개의 작고 독립적인 디스크를 배열로 구성하여 하나의 고성능 디스크처럼 동작하도록 하는 장치임 ∘ 고성능인 저장 장치와 유연하고 동적인 구조의 필요성 문제로 대규모 조직체들은 저장 영역 네트워크(Storage Area Networks : SANs)를 적용하고 있음 ∘ 디스크 내에 파일 조직에는 비순서 및 순서, 해싱, 인덱싱 등의 방법을 사용하고 있음 ∘ 인덱스는 <레코드 키 값, 포인터>로 구성되며, 기본 인덱스, 보조 인덱스, 집중 인덱스, 비집중 인덱스, 밀집 인데스, 희소 인덱스 등의 유형으로 분류할 수 있음 ∘ 데이터베이스에 주로 응용되는 인덱스 구성방법에는 대표적인 B 트리와 B+ 트리가 있으며, B+트리는 인덱스 세트와 순차 세트로 구성됨이 B 트리의 구조와는 차이가 있음 |
■ 참고자료
| 자료명 | 자료설명 |
| • Elmasri. Navathe, Fundamentals of Database System 3rd Edition, Addison-wesley, 2000 • 황규영 외, 데이터베이스 시스템(4판), ITC, 2004 • 이석호, 데이타베이스 시스템, 정익사, 2005 |
• 강의 자료는 저자 Elmasri의 Database System을 주로 참고했으며, 보완 자료로서 저자 이석호의 데이타베이스 시스템의 내용을 참고했음 |
'정보과학 > 데이터베이스특론' 카테고리의 다른 글
| 설계 및 프로그래밍 실습 (0) | 2023.09.04 |
|---|---|
| SQL (1) | 2023.09.03 |
| 관계데이터 모델 (0) | 2023.09.03 |
| 개체-관계(Entity Relationship) 모델 (0) | 2023.09.02 |
| 데이터베이스 개요 (0) | 2023.09.01 |



