728x90
1. 관계 데이터 모델 개념 및 제약 조건
① 관계 데이터 모델의 개념
| ∘관계 모델에서 데이터베이스는 릴레이션(테이블)들의 모임으로 표현됨 ∘릴레이션은 투플 (행, 레코드)들의 집합으로 표현됨 ∘투플은 애트리뷰트(컬럼, 필드, 혹은 속성)들로 구성됨 ∘ER(Entity Relationship) 모델에서의 표현 - 행: 엔티티 혹은 관계에 해당하는 사실을 표현함 - 열: 애트리뷰트들을 표시함 ∘관계 모델에서의 용어 해설 - 행: 투플 - 열: 애트리뷰트(속성) - 테이블: 릴레이션 - 도메인(domain): 원자 값들(atomic values)의 집합 => 도메인은 실제 데이터 타입으로 명시함 (int, char(10), ) - 릴레이션 스키마(Relation Schema) 릴레이션 이름 R과 애트리뷰트 Ai 들의 집합으로 R(A1, A2, ..., An) 로 표기함 예) STUDENT(Name, SSN, BirthDate, Addr) - 릴레이션의 차수(degree): 릴레이션의 애트리뷰트 개수 - 릴레이션 R(A1, A2, ..., An)의 투플 t 는 n-투플이라고 부름 여기서 값들의 (순서화된) 집합 t = <v1, v2, ..., vn>는 값 vi는 dom(Ai)의 한 원소임 - R에 대한 릴레이션 혹은 릴레이션 인스턴스(Relation instance) r(R) 투플의 집합 r(R) = {t1, t2, ..., tm} r(R) ⊆ dom(A1)×...× dom(An) // r(R) 은 실세계의 특정 상태를 반영 |
※ 릴레이션의 예

② 릴레이션의 특성
| ∘릴레이션에서 투플의 순서는 의미가 없음 (투플의 무순서성) - 집합에서 원소의 순서가 무의미한 것과 마찬가지 임 ∘릴레리션에서 똑같은 투플은 존재하지 않음 (투플의 유일성) - 릴레이션은 투플을 원소로 갖는 집합이기 때문임 ∘각 애트리뷰트와 애트리뷰트 값들이 서로 대응될 수 있다면 애트리뷰트 값들의 순서는 중요하지 않을 수 있음 (애트리뷰트의 무순서성) - n-투플은 n 개 값의 리스트이며, 한 투플 내에서 값들의 순서는 중요함(즉, 리스트에서는 원소의 순서는 중요한 의미를 가짐) - 그러나 예를들어, 하나의 투플을 (<애트리뷰트>, <값>) 쌍들의 집합으로 간주하면 애트리뷰트와 값은 서로 대응될 수 있으며, 값의 순서는 중요하지 않음 ∘투플 내의 필드값은 더 이상 나눌 수 없는 원자 값들임 (애트리뷰트의 원자성) - 값을 알 수 없거나 해당되는 값이 없을 때에는 널(null) 이라는 특수 값을 사용함 - ER 모델에서의 다치 애트리뷰트나 복합 애트리뷰트는 관계모델에서는 허용되지 않음 ∘릴레이션의 의미를 살펴보면, 릴레이션 스키마는 선언이며, 그에 해당되는 각 투플은 그 선언에 대한 인스턴스라고 볼 수 있음. 즉 릴레이션 스키마 주장(assertion)에 대한 사실임 |
※ 널(null) 값
| ∘관계 데이터모델에서 널(null)값도 하나의 원자 값으로 취급함 ∘널(null) 값에는 - 한 투플의 어떤 애트리뷰트 값에 대해서 아직 모르는 경우 - 애트리뷰트가 그 대상에 해당되지 않기 때문에 그 값을 명세할 수 없는 경우 |
③ 관계 모델의 표기
| ∘차수가 n인 릴레이션 스키마 R은 R(A1, A2, ..., An)으로 표기하며, 릴레이션 r(R)의 n-투플 t는 t = <v1, v2, ..., vn>으로 표기함(vi는 애트리뷰트 Ai의 값) ∘t[Ai] 또는 t.Ai는 t에서 애트리뷰트 Ai의 값 vi를 가리킴 ∘투플 t의 구성 요소 값(component value)을 t[Ai] = vi (투플 t에 대한 애트리뷰트 Ai의 값)로 표기하며, 마찬가지로 t[Au, Aw, ..., Az]는 애트리뷰트 Au, Aw, ..., Az 의 값을 포함하는 부(sub)-투플을 가리킴 ∘대문자 Q, R, S 등은 릴레이션 이름을 나타냄 ∘소문자 q, r, s 등은 릴레이션 상태를 나타냄 ∘소문자 t, u, v 등은 투플을 나타냄 ∘일반적으로, STUDENT처럼 릴레이션 스키마의 이름은 릴레이션의 현재 투플들의 집합, 즉 현재의 릴레이션 상태를 가리키고, 반면에 STUDENT(Name, SSN, ...)는 릴레이션 스키마를 가리킴 ∘서로 다른 릴레이션에서 동일한 이름의 애트리뷰트를 사용할 수 있으며, 이 경우 애트리뷰트 이름 앞에 릴레이션 이름을 붙여서 서로를 구분함 예) STUDENT.Name, Faculty.name, Employee.name |
※ 키(key)의 유형
| ∘키(key)란 투플을 유일하게 식별할 수 있는 애트리뷰트 집합 ∘후보 키(candidate key) - 릴레이션 R(A1, A2, ..., An)에 대한 애트리뷰트 집합 K={Ai, Aj, ...,Ak} 으로 두 성질은 ① 유일성(uniqueness): 각 투플의 K(={Ai, Aj, ..., Ak})의 값(<vi, vj, ..., vk>)은 유일함 ② 최소성(minimality): K는 투플을 유일하게 식별하기 위한 애트리뷰트로만 구성함 ∘수퍼 키(super key) - 유일성(uniqueness)은 만족하지만 최소성이 만족되는 않는 애트리뷰트의 집합 ∘기본 키(primary key) - 후보 키(candidate key) 중에서 데이터베이스 설계자가 지정한 하나의 키 - 각 투플에 대한 기본 키 값은 항상 유효(no null value)해야 함 ∘대체 키(alternate key) - 후보 키 중에 기본 키를 제외한 나머지 후보 키를 대체키라고 칭함 ∘대리 키(surrogate key) = 인공키 - 키가 너무 길거나 여러개의 속성으로 구성된 경우에 인위적으로 추가한 식별자, ∘복합 키(composite key) - 둘이상의 애트리뷰트를 묶어서 키를 표현한 경우에 복합키라고 칭함 |
④ 관계 모델의 제약 조건
| ∎개체 무결성 제약조건(entity integrity constraints) ∘어떠한 기본 키 값도 널 값을 가질 수 없다는 제약 조건임 ∘기본키가 각 투플들을 식별하는 데에 이용되기 때문임 ∘참고: R의 기본키에 속하지 않는 애트리뷰트들도 null 값을 갖지 않도록 제한할 수 있는데 그 방법은 릴레이션의 속성을 정의할 때 not null 이라고 명시하면 됨 ∎참조 무결성 제약조건(referential integrity constraints) ∘하나의 릴레이션 R에서 속성 F의 값으로 다른 릴레이션 S의 기본 키 P 값을 참조하는 경우에 R과 S는 참조 무결성 제약 조건을 가진다고 함. 이 때, F의 값은 널을 가질 수 있음 ∘t1[F] = t2[P]이면 R의 투플 t1이 S의 투플 t2를 참조한다(reference)고 하며, F를 외래키(foreign key)라고 부름. - R을 참조한(referencing) 릴레이션, S를 참조된(referenced) 릴레이션이라고 부름 ∘일반적으로 참조 무결성은 두 릴레이션에 대한 제약조건임을 언급하지만, 하나의 릴레이션에서도 참조 관계가 형성되어서 참조 무결성 제약 조건이 존재함 ∘데이터베이스 스키마에서 참조 무결성 제약조건은 R1.FK에서 R2로의 화살표로 표시함 ∎도메인 제약 조건(domain constraints) ∘각 애트리뷰트 A의 값은 반드시 A의 도메인 dom(A)에 속하는 원자값이어야 함 ∘도메인과 관련된 데이터 타입 - 정수, 실수와 같은 표준 숫자형 - 문자, 고정길이 문자열, 가변길이 문자열 - 날짜, 시간 - 화폐단위 - 메모 등 ∎키 제약조건(key constraints) ∘기본 키 (primary key) - 릴레이션이 여러 개의 후보키(candidate key)를 가지면 이중 하나를 임의로 선택하여 기본키(primary key)로 지정함 - 기본키를 구성하는 애트리뷰트는 밑줄로 표시함 - 애트리뷰트의 값으로 널의 허용 여부도 중요한 제약 조건임 |
※ 데이터베이스 상태
| ∘데이터베이스 상태 (database state) 란? - 어느 한 시점에 데이터베이스에 저장된 데이터 값 - 데이터베이스 인스턴스, 즉 스키마에 정의된 릴레이션 인스턴스의 집합 - 데이터베이스 상태 변화: 삽입, 삭제, 변경 연산 - DBMS는 데이터베이스 상태의 변화에도 항상 무결성 제약을 만족시키도록 해야 함 |
2. 관계 대수
① 단항관계 연산
| ∎SELECT 연산 (σ로 표기) ∘릴레이션 R에서 어떤 선택조건 c를 만족하는 투플들을 선택함 ∘선택 조건을 만족하는 릴레이션의 수평적 부분집합(horizontal subset)에 해당됨 ∘연산 형식은 σc(R) 로 표현되며, SQL 언어의 “R WHERE 조건식”에 해당됨 ∘선택조건 c는 R의 애트리뷰트들에 대한 임의의 불리언 식임 ∘결과 릴레이션은 R과 동일한 애트리뷰트들을 가짐 ∘결과 릴레이션은 r(R)의 투플 중 애트리뷰트 값들이 조건 c를 만족하는 투플들로 구성됨 ∘선택조건 c에 의해 얻어진 선택된 투플 수의 비율을 그 조건의 선택률(selectivity)라 함 ∘실렉트 연산은 서로 교환적이며, 또한 연속된 연산은 AND 조건으로 결합할 수 있음 σ<조건2>(σ<조건1>(R)) = σ<조건1>(σ<조건2>(R)) = σ<조건1> AND σ<조건2> (R) ∘예) σDNO=4 (EMPLOYEE) σSALARY>30000 (EMPLOYEE) σ(DNO=4 AND SALARY>25000) OR DNO=5 (EMPLOYEE) ∎PROJECT 연산 (Π로 표기) ∘릴레이션 R에서 애트리뷰트 리스트 L에 명시된 애트리뷰트들만 선택함 ∘릴레이션의 수직적 부분집합(vertical subset)에 해당됨 ∘연산 형식은 ΠL(R)로 표현함 ∘결과 릴레이션은 L에 명시된 R의 애트리뷰트들만 가짐 ∘예) ΠFNAME,LNAME,SALARY (EMPLOYEE) ∘PROJECT연산은 결과 릴레이션이 수학적 집합이므로 중복된 투플들을 제거함 ∘예륻 들면 ΠSEX,SALARY (EMPLOYEE)의 결과에서 동일 행의 값이 여러 개 될 경우 릴레이션 특성 상 하나의 투플 만 표현됨 |
※ 연산의 순서와 이름 변경 연산 (ρ: rho)
| ∘다수의 연산을 결합하여 관계 대수식(질의)을 형성할 수 있음 ∘예) 부서 4 에서 일하는 사원들의 이름과 봉급을 검색하라 - ΠFNAME,LNAME,SALARY (σDNO=4 (EMPLOYEE)) ∘각 중간 단계의 임시 릴레이션에 이름을 부여할 수도 있음 ∘DEPT4_EMPS ←σDNO=4 (EMPLOYEE) ∘R ←ΠFNAME,LNAME,SALARY (DEPT4_EMPS) ∘결과 릴레이션의 애트리뷰트 이름은 재명명 할 수도 있음 - 이름 변경 연산 기호는 ρ(rho) ∘DEPT4_EMPS ←σDNO=4 (EMPLOYEE) ∘R(FIRSTNAME, LASTNAME, SALARY) ← ΠFNAME,LNAME,SALARY(DEPT4_EMPS) - FNAME→FIRSTNAME, LNAME→LASTNAME 으로 각각 이름 변경연산을 한 것임 |
② 집합관련 연산
| ∎합집합 (union, ∪) ∘합병 가능한 두 릴레이션 R과 S의 합집합(∪) ∘수학적 표현으로 정리하면, R∪S = { t | t∈R ∨ t∈S } ∘|R∪S| ≤ |R| + |S| - R∪S의 카디널리티는 R과 S 각각의 카디널리티의 합보다 작거나 같음 ∎교집합 (intersect, ∩) ∘합병 가능한 두 릴레이션 R과 S의 교집합(∩) ∘수학적 표현으로 정리하면, R∩S = { t | t∈R ∧ t∈S } ∘|R∩S| ≤ min { |R|, |S| } - R∩S의 카디널리티는 R이나 S 중 어떤 카디널리티 보다도 크지 않음 ∎차집합 (difference, -) ∘합병 가능한 두 릴레이션 R과 S의 차집합(-) ∘수학적 표현으로 정리하면, R-S = { t | t∈R ∧ t ∉ S } ∘|R-S| ≤ |R| - R-S의 카디널리티는 릴레이션 R의 카디널리티보다 크지 않음 ∎카티션 프로덕트 (cartesian product, ×) ∘두 릴레이션 R x S는 R에 속한 투플 r과 S에 속한 투플 s를 접속시킨 r・s라는 투플 집합임 ∘수학적 표현으로 정리하면, R x S = { r・s | r∈R ∧ s∈S } - r・s 에서 “・” 은 접속(concatenation)을 나타냄 ∘|R×S| = |R|×|S| - R × S의 카디널리티는 R의 카디널리티와 S의 카디널리티를 곱한것과 같음 차수(degree) = R의 차수 + S의 차수 |
③ 이항관계 연산(1)
| ∎조인(Join, ⋈) 연산 ∘두 릴레이션으로부터 관련있는 투플을 결합하여 하나의 투플로 생성함 ∘관련성의 여부를 조건으로 표시하며, 이를 조인조건이라고 함 - 조인 조건은 <조건> AND <조건> AND ... AND <조건>로 표기함 - 각 조건의 형태는 Ai θ Bj 이며, Ai는 R의 애트리뷰트, Bj는 S의 애트리뷰트임 - 조인 조건에 사용된 속성 (Ai 와 Bj 를 조인 속성이라고 부름) ∘세타 조인(theta join)이라고 함은 R(X), S(Y), A∈X, B∈Y에 대하여 - R⋈AθBS = { r・s | r∈R ∧ s∈S ∧ ( r.Aθs.B) } - A, B: 조인 애트리뷰트(joining attribute) - θ(theta)는 비교연산자 {=, <, ≤, >, ≥, ≠} 들 중에 하나임 - 결과 차수 = R의 차수 + S의 차수 - 원 소속 릴레이션의 이름을 애트리뷰트 앞에 한정어로 붙여 일관성 유지함 ∘동일 조인(=동등조인, equi join)은 θ의 관계연산자가 = 일 때를 말함 - R⋈A=BS = { r・s | r∈R ∧ s∈S ∧ ( r.A=s.B ) } ∘동일 조인 연산의 예  |
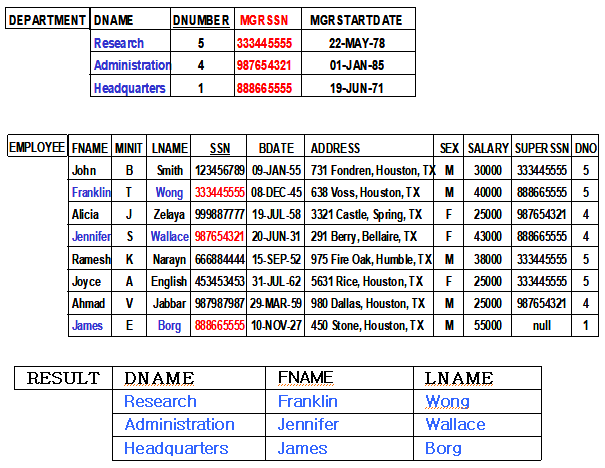
④ 이항관계 연산(2)
| ∘자연 조인 (NATURAL JOIN, *)은 조인 결과에서 조인 속성 하나를 제거하여 중복된 애트리뷰트 값이 나타나지 않도록 한 조인을 말함. 동일조인(EQUI-JOIN)의 경우의 결과에는 두 조인속성의 값이 중복되어 나타남 ∘자연조인에 대한 일반적인 정의: R ← R1*(R1의 조인 애트리뷰트들),(R2의 조인 애트리뷰트들) R2 ∘예제: 모든 EMPLOYEE의 이름과 그의 DEPARTMENT 이름을 검색하라 T ← EMPLOYEE * (DNO),(DNUMBER) DEPARTMENT RESULT ← ΠFNAME,LNAME,DNAME(T) ∘두 조인 속성이 동일한 이름을 갖는다면 간단히 R ← R1* R2라고 표시함 ∘자연 조인에서는 조인 애트리뷰트들이 양쪽의 릴레이션에서 동일한 이름을 가져야 하며, 그렇지 않는 경우 조인 속성의 이름을 먼저 동일하게 변경해야 함 ∘예) “모든 EMPLOYEE의 이름과 그 SUPERVISOR의 이름을 검색하라” SUPERVISOR(SUPERSSN,SFN,SLN)←ΠSSN,FNAME,LNAME(EMPLOYEE) // 속성명 변경 T ← EMPLOYEE * SUPERVISOR // 자연조인 RESULT ← ΠFNAME,LNAME,SFN,SLN(T) ∘자연조인의 표기를 “ * ” 대신에 “⋈N”으로 표기된 참고서적도 많이 있음 ∘예) "모든 EMPLOYEE의 이름과 그가 일하는 DEPARTMENT의 이름을 검색하라" PROJ_DEPT ← PROJECT * ρ(DNAME, DNUM, MGRSSN, MGRSTARTDATE)(DEPARTMENT) 중간결과 테이블을 별도로 설정하면, DEPT ← ρ(DNAME, DNUM, MGRSSN, MGRSTARTDATE)DEPARTMENT // DNUMBER→DNUM PROJ_DEPT ← PROJECT * DEPT ∘Self JoinS은 한 릴레이션을 두 개의 릴레이션을 만들어서 조인하는 방법을 말하며, 이때 사본 릴레이션에서는 원본 애트리뷰트 이름을 재명명(renaming)하는 것이 유용함 ∘예) "모든 EMPLOYEE의 이름과 그의 SUPERVISOR의 이름을 검색하라" SUPERVISOR(SSN2,SFN,SLN) ← ΠSSN,FNAME,LNAME(EMPLOYEE) T ← EMPLOYEE ⋈ SUPERSSN=SSN2 SUPERVISOR // 동일 조인 RESULT ← ΠFNAME,LNAME,SFN,SLN(T) |
⑤ 이항관계 연산(3)
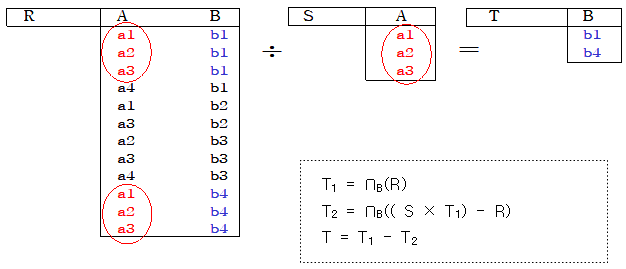
| ∎디비전(Divion, ÷) 연산 ∘R(Z) ÷ S(X) 디비전 연산은 두 릴레이션 R(Z), S(X) 에 대하여 X⊆Z이고 Y = Z - X 이다. 즉, Y는 R의 애트리뷰트 중에서 S의 애트리뷰트가 아닌것들의 집합임 - R(X) = R(Y, Z) 로 표현할 수 있음 . T1 = ΠY(R) . T2 = ΠY(( S × T1) - R) . T = T1 - T2 ∘R ÷ S를 수학적 표현으로 정리하면, { t | t∈ΠY(R) ∧ t・s∈R for all s∈S } ∘결과 릴레이션에 속하는 각 투플에 대해 릴레이션 S에 모든 투플과 접속시키면 투플 전부가 릴레이션 R에 속해 있는 투플과 같아야 하는 특성이 있음 (R ÷ S) × S ⊆ R |
※ 관계 대수 연산의 완전 집합
| ∘연산자 집합 {σ, Π, ∪,-, ×}를 관계대수 연산자의 완전 집합(complete set)이라 하며, 다른 모든 관계 대수 연산은 이 집합의 연산들의 조합으로 표현할 수 있음 ∘교집합 연산은 합집합 연산과 차집합 연산을 이용하여 표현할 수 있음 R∩S ≡ (R∪S) - ((R-S) ∪ (S-R)) ≡ R- (R - S) ≡ S - (S - R) ∘조인 연산은 카티션 곱 연산과 실렉트 연산으로 표기 가능함 R⋈AθBS ≡ σAθB(R×S) ∘디비전 연산은 카티션 곱 연산과 차집합 연산을 이용하여 표현할 수 있음 R(Z,Y)÷S(Y) ≡ R[Z] - ((R[Z]×S) - R)[Z] |
⑥ 추가적인 연산구문
| ∎집계함수 (aggregate functions) ∘SUM, COUNT, AVERAGE, MIN, MAX 함수를 의미함 ∘집계함수의 연산 표현은 다음과 같고, 그 중에 그룹화 애트리뷰트들은 선택적임 <그룹화 애트리뷰트들> F <함수 리스트> (R) ∘예1) 모든 사원의 평균 봉급을 검색하라(그룹화 불필요) R(AVGSAL) ← F AVERAGESALARY (EMPLOYEE) ∘예2) 각 부서에 대하여, 부서번호와 부서별 사원수와 평균봉급을 검색하라 R(DNO,NUMEMPS,AVGSAL) ← DNO F COUNTSSN, AVERAGESALARY(EMPLOYEE) DNO를 그룹화 애트리뷰트(grouping attribute)라고 부름 ∎외부조인(OUTER JOIN) ∘정규 EQUIJOIN이나 자연조인(NATURAL JOIN) 연산에서 조인 조건을 만족하지 않은 투플들은 결과 릴레이션에도 나타나지 않는데, 조인에 참여하는 릴레이션의 모든 투플들이 조인의 여부와 관계없이 결과 릴레이션에 나타내고 싶은 경우 외부조인을 사용함 ∘외부조인에서는 상대방 릴레이션에 대응되는 투플이 없으면 빈 애트리뷰트들에 NULL 값을 채워서 결과에 포함시킴 ∘외부조인의 종류 - 왼쪽 외부조인(LEFT OUTER JOIN): R1 +⋈ R2 R1의 모든 투플 결과 나타내도록 함 - 오른쪽 외부조인(RIGHT OUTER JOIN): R1 ⋈+ R2 R2의 모든 투플 결과 나타냄 - 완전 외부 조인(FULL OUTER JOIN): R1 +⋈+ R2 R1과 R2의 모든 투플 결과 나타냄 ∎외부 합집합 (outer union) ∘호환성이 없는 두 릴레이션을 합집합하는데 사용됨 ∘예) STUDENT(Name, SSN, Department, Advisor)와 FACULTY(Name, SSN, Department, Rank)의 outer union은 RESULT(Name, SSN, Department, Advisor, Rank) 임 ∘RESULT 에서 STUDENT 투플은 Rank 속성의 값이 null이고, FACULTY 투플은 Advisor 속성의 값이 null로 나타남 |
※ 세미 조인(Semi-Join, ⋉)
| ∘R(X), S(Y) 의 조인 애트리뷰트를 Z=X∩Y 라 하면, R ⋉ S ≡ R⋈N(ΠZ(S)) ≡ ΠX(R⋈NS) ∘S와 자연조인을 할 수 있는 R의 투플 ∘세미 조인의 특징 R ⋉ S ≠ S ⋉ R R ⋈N S ≡ (R ⋉ S) ⋈N S ≡ (S ⋉ R) ⋈N R |
3. 관계 해석
① 관계 해석의 의미
| ∘관계 해석이란 "어떻게 검색할 것인가" 보다 "무엇을 검색할 것인가" 만을 기술하는 선언적 표현법을 사용하는 비절차적 질의어에 속함 ∘SQL을 포함한 많은 상업용 관계 언어들이 관계 해석에 기반을 두고 있음 ∘투플 관계 해석(tuple relational calculus)과 도메인 관계 해석(domain relational calculus)으로 구분됨 ∘관계 대수와의 차이점은 관계 해석은 하나의 선언적(declarative) 해석식으로 검색 질의를 명시하는 비절차적인 언어이며, 관계 대수에서는 연산들을 순차적으로 사용하므로 절차적인 성질을 가짐 ∘관계 대수와 표현력(expressive power)은 동등 ∘어떤 관계 질의어 L이 관계 해석 또는 관계 대수로 표현 가능한 어떤 질의도 표현할 수 있으면 L은 관계적으로 완전(relationally complete)하다고 함 ∘대부분의 관계 질의어들은 관계적으로 완전하며, 집단 함수(aggregate functions), 그룹화(grouping), 순서화(ordering) 등의 연산들을 제공하므로 관계 해석보다 표현력이 강함 |
※ 프리디킷(predicate)
| ∘프리디킷(predicate)란 어떤 객체(object)의 성질이나 객체와 객체 간의 관계를 표현한 것으로서, 객체 x의 성질에 관한 프리디킷을 p(x)로 표기함 ∘predicate → a function whose value is true or false ∘프리디킷(predicate)을 우리말로 표현하면 ‘술어’라고 함 ∘예1) “나는 키가 크다”는 명제에서 ‘키가 크다’는 것은 ‘나’라는 객체의 성질을 표현한 술어이기에 ‘나’를 객체 x,라고 할때 술어 ‘키가 크다’는 p(x)가 됨 ∘예2) “x2=9를 만족하는 정수 x가 존재한다”는 명제는 ‘어떤 수의 제곱은 9’라고 하는 특정 성질을 만족하는 객체(‘어떤 정수’)의 존재를 한정하는 것임→ 술어 한정자 표현:∃x[p(x)] ∘∃x[p(x)]: p(x)를 만족하거나 성립하는 x가 존재함 ∘∀x[p(x)]: 모든 x에 대하여 p(x)가 성립함 |
② 투플 관계 해석
| ∎투플변수의 표현 ∘투플 변수는 릴레이션의 투플들을 범위(range)로 가지는 변수임 ∘예) 봉급이 $50,000를 넘는 모든 사원을 검색하라 {t | EMPLOYEE(t) and t.SALARY > 50000 } - EMPLOYEE(t)는 투플 변수 t가 릴레이션 EMPLOYEE의 투플들을 범위로 함을 나타냄 - 투플 t에 대하여 t.SALARY > 50000을 만족하는 투플 만이 검색됨 - 투플 t의 모든 애트리뷰트 값들이 리턴됨 ∘투플 t의 일부 애트리뷰트 만을 검색하려면 다음과 같이 작성함 {t.FNAME, t.LNAME | EMPLOYEE(t) and t.SALARY > 50000 } - 이것은 다음 SQL 질의와 동일한 의미를 가짐 SELECT T.FNAME, T.LNAME FROM EMPLOYEE T WHERE T.SALARY > 50000; ∎투플 관계해석의 표현과 식 ∘투플 관계해석의 일반식 형태 {t1.A1, t2.A2, ..., tn.An | COND(t1, t2, ..., tn, tn+1, tn+2, ..., tn+m) } - t1, t2, ..., tn, tn+1, tn+2, ..., tn+m은 투플 변수 - 각 Ai는 ti가 범위로 하는 릴레이션의 애트리뷰트 - COND는 조건 또는 투플 관계 해석의 식(formula) ∘식(formula)은 다음과 같은 원자(atoms)들로 이루어짐 - Ri(ti)는 ti의 범위가 Ri임을 명시 - (ti.A op tj.B), op는 비교 연산자 (=, <, ≤, ...) - (ti.A op c) 또는 (c op tj.B), c는 상수 ∘각 원자는 특정한 투플들의 조합에 대해서 참(true) 또는 거짓(false)으로 계산되며, 계산된 결과값을 원자의 진리값이라 부름 ∘식(formula): and, or, not으로 연결된 원자들 - 모든 원자들은 식이라고 봄 - F1과 F2가 식이면 (F1 and F2), (F1 or F2), not(F1), not(F2)도 식이라고 봄 |
② 정량자가 포함된 식의 의미와 그 예(1)
| ∎존재 정량자와 전체 정량자의 개념 ∘정량자(quantifiers)가 식에 사용될 수 있음 - 전체 정량자(universal quantifier) (∀) (for all이라 읽음) - 존재 정량자(existential quantifier) (∃) (their exists라 읽음) ∘자유 (free) 투플 변수와 속박 (bound) 투플 변수 - 어떤 식 F가 원자인 경우, 여기에 나타난 투플 변수의 어커런스(occurrence)는 F에서 자유로움 (자유 투플 변수) - 식 (F1 and F2), (F1 or F2), not(F1), not(F2)에 나타난 투플 변수 t가 자유로운가 여부는 F1이나 F2에서 자유로운가에 달려있음 - F내의 투플 변수 t의 모든 자유 어커런스들은 F' = (∃t)(F) 나 F' = (∀t)(F) 형태의 식에서 정량자에 속박됨 ∘예) F1: d.DNAME = 'Research' F2: (∃t)(d.DNUMBER = t.DNO) ∘d 는 F1과 F2 모두에서 자유지만, t는 F2에서 ∃ 정량자에 속박됨 ∎정량자가 포함된 식의 진리값 계산 ∘F가 식이면, (∃t)(F)도 식임 ∘F내의 t의 자유 어커런스들에 할당된 "적어도 하나의 투플"에 대해서 F가 참으로 계산되면 식 (∃t)(F)는 참이고, 그렇지 않으면 거짓임 ∘F가 식이면, (∀t)(F)도 식임 ∘F 내의 t의 자유 어커런스들에 할당된 "모든 투플"에 대해서 F가 참으로 계산되면 식 (∀t)(F)는 참이고, 그렇지 않으면 거짓임 ∘F가 참이 되게 하는 어떤 투플 t가 존재하면 (∃t)(F)가 참이므로, ∃를 존재정량자라 부름 ∘"모든" 투플들이 F를 참이 되도록 해야 (∀t)(F)가 참이므로, ∀를 전체 정량자라 부름 ∎존재 정량자의 질의 예 ∘질의: 'Research' 부서에서 일하는 모든 사원의 이름과 주소를 검색하라 Q1: {t.FNAME, t.LNAME, t.ADDRESS | EMPLOYEE(t) and (∃d) (DEPARTMENT(d) and d.DNAME='Research' and d.DNUMBER=t.DNO)} - 관계 해석 식에서 자유 투플 변수들만 막대 ( | ) 왼쪽에 나타냄 - 막대 ( | )는 "such that"이라 읽음 - EMPLOYEE(t), DEPARTMENT(d)는 t와 d의 범위 릴레이션을 명시함. - d.DNAME='Research'는 선택 조건(selection condition)임 (관계대수 SELECT 해당) - d.DNUMBER=t.DNO는 조인 조건(join condition)임 (관계대수 EQUI-JOIN과 유사함) |
③ 정량자가 포함된 식의 의미와 그 예(2)
| ∎전체 정량자의 질의 예 ∘전체 정량자를 사용할 때 식이 의미를 갖도록 하기 위하여 몇가지 규칙을 따라야 함 ∘질의: 5번 부서에 의해 관리되는 모든 프로젝트들에 참여하는 사원들의 이름을 찾아라 Q2: {e.LNAME, e.FNAME | EMPLOYEE(e) and ((∀x) (not (PROJECT(x)) or (not (x.DNUM = 5) or ((∃w) (WORKS_ON(w) and w.ESSN = e.SSN and x.PNUMBER = w.PNO)))))} ∘Q2의 기본 구성요소들 - Q2: {e.LNAME, e.FNAME | EMPLOYEE(e) and F'} - F' = (∀x) (not(PROJECT(x)) or F1) - F1 = (not(x.DNUM = 5) or F2) - F2 = (∃w) (WORKS_ON(w) and w.ESSN = e.SSN and x.PNUMBER = w.PNO) ∘Q2의 설명 - Q2의 결과로 구해지는 사원 e는 5번 부서에서 관리하는 모든 프로젝트에서 근무해야함 - 이러한 푸플을 찾기 위하여 관심없는 모든 투플들을 전체 정량자로부터 제외시켜야 함 - F'에서, not(PROJECT(x))는 관심있는 릴레이션 "PROJECT"에 없는 모든 투플들에 대해 x를 참으로 만듬 - F1에서, not(x.DNUM = 5)는 관심없는 PROJECT 투플들, 즉 "DNUM이 5가 아닌 투플들"에 대해 x를 참으로 만듬 - F2는 나머지에 대해 만족되어야 할 조건, 즉 "5번 부서에 의해 관리되는 모든 PROJECT 투플들" 을 명시함 |
※ 전체 정량자와 존재 정량자 사이의 변환
| ∘수학적 논리로부터 유래된 잘 알려진 변환법 (∀x) (P(x)) ≡ (not∃x) (not(P(x))) (∃x) (P(x)) ≡ not(∀x) (not(P(x))) (∀x) (P(x) and Q(x)) ≡ (not∃x) (not(P(x)) or not(Q(x))) (∀x) (P(x) or Q(x)) ≡ (not∃x) (not(P(x)) and not(Q(x))) (∃x) (P(x) or Q(x)) ≡ not(∀x) (not(P(x)) and not(Q(x))) (∃x) (P(x) and Q(x)) ≡ not(∀x) (not(P(x)) or not(Q(x))) ∘다음 식들이 성립함 (⇒는 내포(implies)를 나타냄) (∀x) (P(x)) ⇒ (∃x) (P(x)) (not∃x) (P(x)) ⇒ not(∀x) (P(x)) ∘그러나, 다음은 성립하지 않음 not(∀x) (P(x)) ⇒ (not∃x) (P(x)) |
④ 도메인 관계 해석
| ∘투플 변수 대신 도메인 변수(domain variables)를 사용하는 관계 해석임 ∘도메인 변수는 한 애트리뷰트의 도메인을 범위로 가짐 ∘차수가 n인 릴레이션의 경우 n 개의 도메인 변수를 사용함 ∘질의 예1) 이름이 'John B. Smith'인 사원의 생일과 주소를 검색하라 Q1: {uv | (∃q) (∃r) (∃s) (EMPLOYEE(qrstuvwxyz) and q = 'John' and r = 'B' and s = 'Smith') } - EMPLOYEE의 각 애트리뷰트들을 위한 열 개의 도메인 변수들: qrstuvwxyz - BDATE를 위한 변수 u, ADDRESS를 위한 v - 조건에 참여하는 변수들 q(FNAME), r(MINIT), s(LNAME) - 조건에 참여하는 변수들 (q, r, s)만 존재 정량자로 속박함 ∘또 다른 표기법(QBE에서 사용): Q1': {uv | EMPLOYEE('John', 'B','Smith',t,u,v,w,x,y,z) } ∘질의 예2) 'Research' 부서에서 일하는 모든 사원들의 이름과 주소를 검색하라 Q2: {qsv | (∃z) (EMPLOYEE(qrstuvwxyz) and (∃l) (∃m) (DEPARTMENT(lmno) and l = 'Research' and m = z)) } - (m = z)는 조인 조건 - (l = 'Research')는 선택 조건 ∘질의 예3) 'Stafford'에 위치한 모든 프로젝트에 대해서 프로젝트 번호와 부서 번호, 그리고 부서 관리자의 성, 생일, 주소를 나열하라 Q3: {iksuv | (∃j) (PROJECT(hijk) and (∃t) (EMPLOYEE(qrstuvwxyz) and (∃m) (∃n) (DEPARTMENT(lmno) and k = m and n = t and j = 'Stafford'))) } |
'정보과학 > 데이터베이스특론' 카테고리의 다른 글
| 설계 및 프로그래밍 실습 (0) | 2023.09.04 |
|---|---|
| SQL (1) | 2023.09.03 |
| 저장장치 구조 (4) | 2023.09.02 |
| 개체-관계(Entity Relationship) 모델 (0) | 2023.09.02 |
| 데이터베이스 개요 (0) | 2023.09.01 |



